概要
時間計算量について調べます
ソートアルゴリズムなどを解説するにあたって時間計算量についての概念が重要になるため今のうちにまとめておきます
時間計算量について
計算量とは、
「そのプログラムがどれくらい速いかを大雑把に表す指標」
です。もう少し正確に言うと、
「入力サイズの増加に対して、実行時間がどれくらいの割合で増加するかを表す指標」
です。
プログラムの処理時間というのは実行するコンピュータの環境に依存してしまうため、時間計算量は「実行ステップ数」により表されます。これはプログラムを書く際に記述するif文やwhile文の制御構文を組み合わせた結果、大雑把にどれくらいのステップがかかるのかという指標になります。
オーダーについて
計算量は「オーダ」とも呼ばれ、評価するとための式としてを_O_記法使って表している
_O_記法は_O(n)_や_O(n2)_のような形で記述
代表的な計算量の例として
| 表記 | 例 |
|---|---|
| O(1) | ハッシュ |
| O(log n) | 1回探索するたびに1/nに要素を絞り込める(二分探索、詳しくは後述) |
| O(n) | 1つづつ全要素探索する(線形探索) |
| O(n log n) | クイックソート |
| O(n2) | 2重ループを伴うアルゴリズム、バブルソートなど |
O(n)について簡単に説明する
問題:2,3,6,9,15という5つの数字の中で9という数字を見つける
プログラム実装例:先頭から順に調べていくアルゴリズム(線形探索という)を組んだ場合
- 2 -> 違う
- 3 -> 違う
- 6 -> 違う
- 9 -> 見つけた!!!
基本的にO記法というのはそのアルゴリズムで一番ステップ数がかかる時のことを書くため
n個の要素に対して最悪n回の試行が必要になる、従ってこのアルゴリズムはO(n)
という考え方となる
対数について
logの式が何を表すのかというと_log10 100_は10を何乗したら100になるのかということ
対数がアルゴリズムにどう使われるのかということの簡単な例として_log2 n_を説明する
_log2 n_になるアルゴリズムの例としては二分探索がある、二分探索のイメージ図は以下
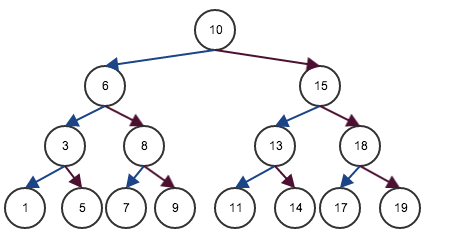
1,3,5,6,7,8,9,10,15,11,13,14,15,17,18,19という適当な数の集合から特定の値を見つける時に、上記の図のようなツリー構造を作っていれば
14を見つける時は10->15->13->14と4回の比較で到達できる
大きいか小さいかで判断することから1回の操作で1/2程度の要素に絞ることができる
今回、整数の数は16(入力数が16)の中で探すことになるので1/2になる探索を何回繰り返せば16になるのかということで
2を何乗したら16になるのかということで
log2 16 = 4
従って最大で4回の試行ができるということでこのアルゴリズムは_log2 n_ということになる
この探索方法はひとつづつ全要素調べる_O(n)_よりも高速だということがわかる
オーダーの比較
簡単にどういうアルゴリズムが優秀なのかを比較してみる
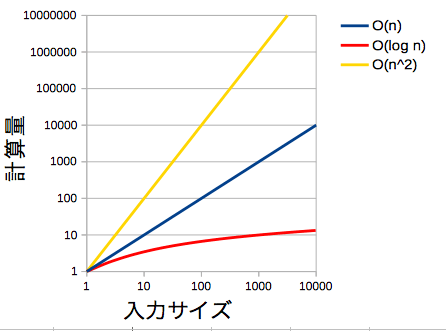
_O(n2)_は時間がかかってしまうことがわかる
O(1)という理想のアルゴリズムハッシュについて
ハッシュは実質_O(1)_という理想のアルゴリズム
しかし考えなければならないことが多い
例えば名前(キー)を元に学生番号(値)を求める場合
array['hoge hanako'] -> 学生番号110 array['hoge taro'] -> 学生番号111 array['suzuki hoge'] -> 学生番号125
というハッシュ配列を作成しておけば名前を入力することで全て1ステップで学生番号を得ることができる
しかし人数が極論10兆人になった場合、配列の要素数には限界があってPHP5系だと4294967296(2^32)個までしか登録できないのでプログラムでエラーを起こしてしまう
またもう一つの問題として同じ名前の人が複数人いた場合をどうするのかを考えなければならない
従って実質_O(1)_だが考えることが多いのがハッシュの課題点である
コメントを書く
コメント一覧